ATOC 4815/5815

Numerical Integration & Explicit Euler

Will Chapman

CU Boulder ATOC

2026-01-01

Numerical Integration

Today’s Objectives

  • Understand when and why we need numerical integration
  • Master the Explicit Euler method for solving ODEs
  • Apply Euler method to atmospheric science problems
  • Prepare for implementing Lorenz63 model (midterm!)

Reminders

Midterm Coming Soon!

  • Focus: NumPy, Python fundamentals, Explicit Euler
  • Practice: Lorenz63 class structure

Office Hours:

Will: Tu 11:15-12:15p Th 9-10a Aerospace Cafe

Aiden: M / W 330-430p DUAN D319

DUAN Building

ATOC 4815/5815 Playlist

Spotify Playlist: ATOC4815

  • This Lecture:

Artificial Light by Typhoon

Why Numerical Integration?

Earth Science is Full of DiffEqs

Temperature evolution: \[\frac{dT}{dt} = -\alpha(T - T_{env}) + H\]

Wind acceleration: \[\frac{du}{dt} = -\frac{1}{\rho}\frac{\partial p}{\partial x} + fv\]

Lorenz63 chaotic system: \[\frac{dx}{dt} = \sigma(y - x)\] \[\frac{dy}{dt} = \rho x - y - xz\] \[\frac{dz}{dt} = xy - \beta z\]

What Does It Mean to “Solve” an DiffEq?

Say we have an initial value problem:

\[\frac{dy}{dt} = f(t, y), \quad y(t_0) = y_0\]

Goal: Find the trajectory \(y(t)\) for \(t > t_0\)

Two options:

  1. Analytical integration → exact equation for \(y(t)\)
  2. Numerical integration → approximation for \(y(t)\)

Analytical Integration: The Dream

Example: Simple exponential decay

\[\frac{dT}{dt} = -\alpha T, \quad T(0) = T_0\]

Analytical solution:

\[T(t) = T_0 e^{-\alpha t}\]

Perfect! We have an exact formula for any time \(t\).

Analytical Integration: The Reality

Lorenz63 equations:

\[\frac{dx}{dt} = \sigma(y - x)\] \[\frac{dy}{dt} = \rho x - y - xz\] \[\frac{dz}{dt} = xy - \beta z\]

No analytical solution exists! 😱

Most real-world systems do not have analytical solutions.

We need numerical methods.

Numerical Integration: The Only Option

Key insight: Most real-world systems cannot be solved analytically

Good news: Extensive research and software tools exist!

  • Many methods optimized for different problems
  • Industry applications drive development
  • Python has excellent tools (scipy, numpy)

Explicit Euler Method

The Big Idea

Can’t solve exactly? Approximate step by step!

Replace derivative \(\frac{dy}{dt}\) with finite difference:

\[\frac{dy}{dt} \approx \frac{y_{n+1} - y_n}{\Delta t}\]

Substitute into ODE:

\[\frac{y_{n+1} - y_n}{\Delta t} = f(t_n, y_n)\]

Explicit Euler Formula

Rearrange to solve for \(y_{n+1}\):

\[y_{n+1} = y_n + f(t_n, y_n) \cdot \Delta t\]

Where:

  • \(y_n\) = state at current time step \(n\)
  • \(y_{n+1}\) = state at next time step \(n+1\)
  • \(f(t_n, y_n)\) = tendency (rate of change)
  • \(\Delta t\) = time step size

Visual Interpretation: Forward Euler

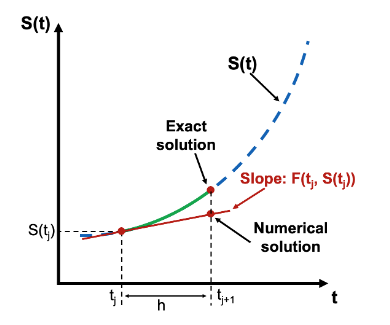
Key idea: Use the slope \(F(t_i, S(t_i))\) at the current point to step forward

  • Exact solution: True trajectory (blue curve)
  • Numerical solution: Approximate trajectory using tangent line (red segments)
  • Error accumulates: Each step introduces small error

Simple Example: Exponential Decay

\[\frac{dT}{dt} = -0.5T, \quad T(0) = 100, \quad \Delta t = 0.1\]

Step 1: \[T_1 = T_0 + f(t_0, T_0) \cdot \Delta t = 100 + (-0.5 \times 100) \times 0.1 = 95\]

Step 2: \[T_2 = T_1 + f(t_1, T_1) \cdot \Delta t = 95 + (-0.5 \times 95) \times 0.1 = 90.25\]

Step 3: \[T_3 = T_2 + f(t_2, T_2) \cdot \Delta t = 90.25 + (-0.5 \times 90.25) \times 0.1 \approx 85.74\]

Implementing Euler in Python

import numpy as np

def euler_step(y, f, dt):
    """One step of Explicit Euler
    
    Args:
        y: current state
        f: tendency function (returns dy/dt)
        dt: time step
    
    Returns:
        y_next: state at next time step
    """
    tendency = f(y)
    y_next = y + tendency * dt
    return y_next

Full Integration Loop

def integrate(y0, f, dt, n_steps):
    """Integrate ODE using Explicit Euler
    
    Args:
        y0: initial condition
        f: tendency function
        dt: time step
        n_steps: number of time steps
    
    Returns:
        trajectory: array of states over time
    """
    trajectory = [y0]
    y = y0
    
    for step in range(n_steps):
        y = euler_step(y, f, dt)
        trajectory.append(y)
    
    return np.array(trajectory)

Lorenz63 with Explicit Euler

The Lorenz63 System

Edward Lorenz (1963) explored deterministic chaos with:

\[\frac{dx}{dt} = \sigma(y - x)\] \[\frac{dy}{dt} = \rho x - y - xz\] \[\frac{dz}{dt} = xy - \beta z\]

Standard parameters: \(\sigma = 10\), \(\rho = 28\), \(\beta = 8/3\)

Typical initial condition: \((x_0, y_0, z_0) = (1, 1, 1)\)

Applying Euler to Lorenz63

Step 1: Define tendency function

def lorenz_tendency(state, sigma=10, rho=28, beta=8/3):
    """Calculate dx/dt, dy/dt, dz/dt"""
    x, y, z = state
    
    dx_dt = sigma * (y - x)
    dy_dt = rho * x - y - x * z
    dz_dt = x * y - beta * z
    
    return np.array([dx_dt, dy_dt, dz_dt])

Applying Euler to Lorenz63 (cont.)

Step 2: Time step with Euler

def lorenz_step(state, dt):
    """Advance Lorenz63 by one time step"""
    tendency = lorenz_tendency(state)
    state_next = state + tendency * dt
    return state_next

That’s it! This is what you’ll implement for the midterm.

Lorenz63 Class Structure

class Lorenz63:
    def __init__(self, sigma=10, rho=28, beta=8/3, dt=0.01):
        self.sigma = sigma
        self.rho = rho
        self.beta = beta
        self.dt = dt
    
    def tendency(self, state):
        """Calculate derivatives"""
        x, y, z = state
        dx_dt = self.sigma * (y - x)
        dy_dt = self.rho * x - y - x * z
        dz_dt = x * y - self.beta * z
        return np.array([dx_dt, dy_dt, dz_dt])
    
    def step(self, state):
        """One Euler step"""
        return state + self.tendency(state) * self.dt
    
    def integrate(self, state0, n_steps):
        """Full integration"""
        trajectory = [state0]
        state = state0
        for _ in range(n_steps):
            state = self.step(state)
            trajectory.append(state)
        return np.array(trajectory)

Midterm Prep: Logistic Growth

The Logistic Growth Model

Midterm Problem: Population growth with carrying capacity

\[\frac{dN}{dt} = r \cdot N \cdot \left(1 - \frac{N}{K}\right)\]

Where:

  • \(N\) = population at time \(t\)
  • \(r\) = growth rate
  • \(K\) = carrying capacity
  • \(\frac{dN}{dt}\) = rate of change of population

Deriving the Time Stepping Equation

Start with Euler formula: \[N_{n+1} = N_n + f(N_n) \cdot \Delta t\]

Substitute tendency function: \[N_{n+1} = N_n + r \cdot N_n \cdot \left(1 - \frac{N_n}{K}\right) \cdot \Delta t\]

This is your time stepping equation!

Logistic Growth Class Structure

class LogisticGrowth:
    def __init__(self, r, K, dt):
        """Initialize with growth rate, carrying capacity, time step"""
        self.r = r
        self.K = K
        self.dt = dt
    
    def tendency(self, N):
        """Calculate dN/dt given current population"""
        return self.r * N * (1 - N / self.K)
    
    def step(self, N):
        """Advance population by one time step"""
        dN_dt = self.tendency(N)
        N_next = N + dN_dt * self.dt
        return N_next
    
    def integrate(self, N0, n_steps):
        """Evolve population over multiple time steps"""
        trajectory = [N0]
        N = N0
        for _ in range(n_steps):
            N = self.step(N)
            trajectory.append(N)
        return trajectory

Midterm Prep: Key Concepts

  1. Understand the Euler formula: \[y_{n+1} = y_n + f(t_n, y_n) \cdot \Delta t\]

  2. Know the method structure:

    • __init__() → store parameters
    • tendency() → calculates \(f(y)\)
    • step() → applies Euler formula
    • integrate() → loops through time

  3. Practice deriving time stepping equations

  4. Be able to write pseudo code (logic over syntax)

Accuracy and Stability

Numerical vs Analytical Solutions

Key insight: Numerical integration is always an approximation

Accuracy depends on:

  • Time step size \(\Delta t\)
  • The method used (Euler is simplest, not most accurate)
  • The problem being solved
  • Stability of the system

Smaller \(\Delta t\) generally gives better accuracy

Time Step Size Matters

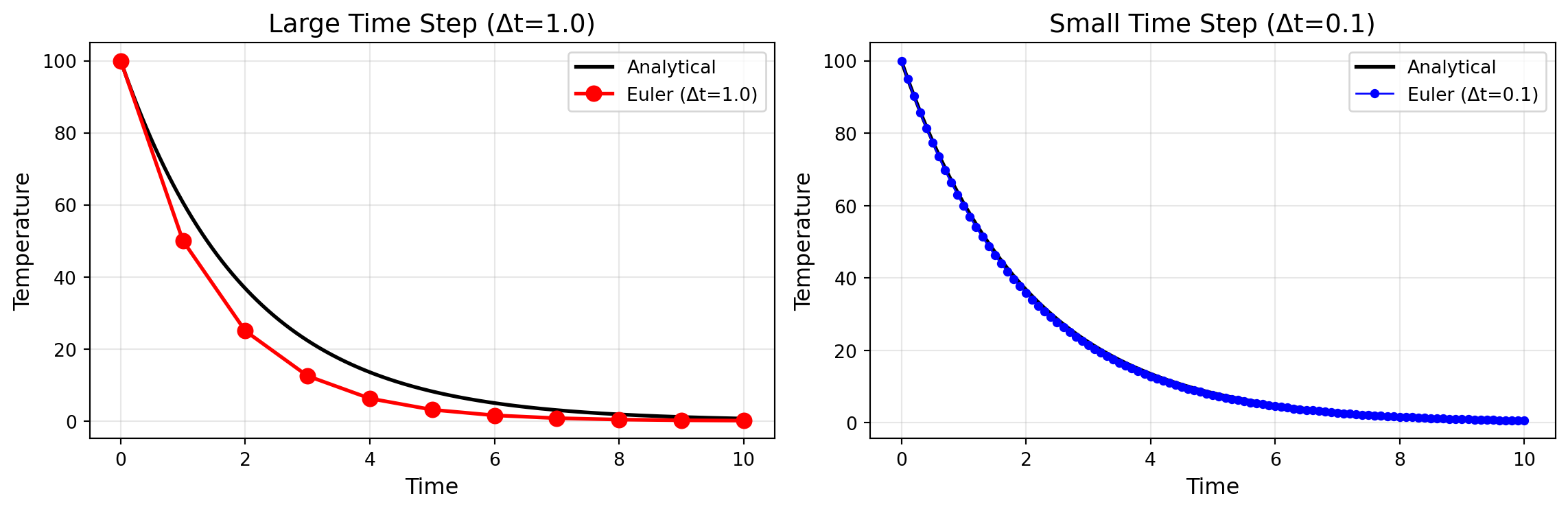
The Stability Question

Apply Euler to the linear test equation \(\;\dfrac{dy}{dt} = \lambda\, y\):

\[y_{n+1} = y_n + \Delta t\,\lambda\, y_n = \underbrace{(1 + \Delta t\,\lambda)}_{G}\; y_n\]

\(G = 1 + \Delta t\,\lambda\) is the amplification factor.

After \(n\) steps: \(\;y_n = G^n\, y_0\).

Stability criterion: \(\;|G| \le 1\)

  • \(|G| < 1\): solution decays (stable)
  • \(|G| = 1\): solution neither grows nor decays (neutral)
  • \(|G| > 1\): solution blows up (unstable)

Stability for Decay (\(\lambda < 0\))

Let \(\lambda = -a\) with \(a > 0\), so \(G = 1 - a\Delta t\).

Regime Condition Behavior
Smooth decay \(0 < a\Delta t < 1\) Monotone convergence to 0
One-step kill \(a\Delta t = 1\) Jumps to 0 in one step
Oscillating decay \(1 < a\Delta t < 2\) Sign flips each step, amplitude shrinks
Blow-up \(a\Delta t > 2\) Sign flips, amplitude grows

Stability rule for Forward Euler on decay:

\[\boxed{\Delta t < \frac{2}{a}}\]

Seeing Stability Break

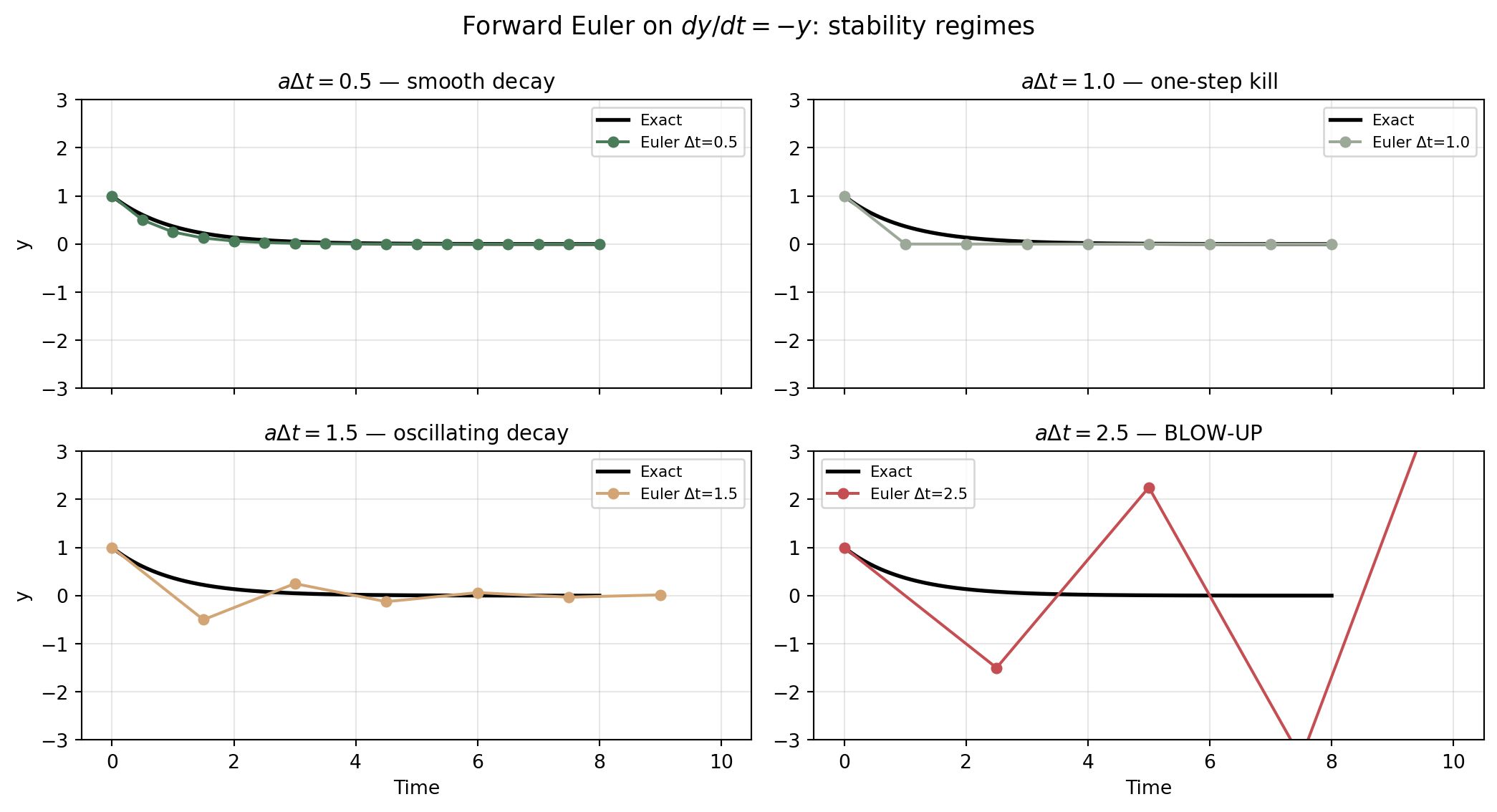
The Stability Rule

For \(\;\dfrac{dy}{dt} = -a\,y\;\) (\(a > 0\)), Forward Euler is stable when:

\[\Delta t < \frac{2}{a}\]

Physical intuition: Faster dynamics (larger \(a\)) demand smaller time steps.

  • \(a = 1 \;\Rightarrow\; \Delta t < 2\)
  • \(a = 100 \;\Rightarrow\; \Delta t < 0.02\)
  • \(a = 10^6 \;\Rightarrow\; \Delta t < 2\times10^{-6}\)

This is why weather models use small time steps!

The atmosphere contains processes with very different time scales.

When Euler Always Fails

Inertial Motion on an f-Plane

1) Setup and assumptions

We consider a parcel moving on an f-plane (constant Coriolis parameter \((f)\)) with:

  • no pressure gradient force
  • no friction
  • horizontal velocity components \((u(t))\) (east) and \((v(t))\) (north)

So the only acceleration is due to the Coriolis force:

\[ \frac{du}{dt} = f\,v, \qquad \frac{dv}{dt} = -f\,u \]

Physical meaning: the acceleration is always perpendicular to the velocity (it turns the flow but does not speed it up).

Why the motion is perpendicular (10 seconds)

Let the horizontal velocity vector be

\[ \mathbf{u} = (u, v) \]

From the inertial (pure Coriolis) equations,

\[ \frac{d\mathbf{u}}{dt} = (f v,\,-f u) \]

Now take the dot product of velocity with its acceleration:

\[ \mathbf{u}\cdot\frac{d\mathbf{u}}{dt} = (u, v)\cdot(fv, -fu) = u(fv) + v(-fu) = fuv - fuv = 0 \]

Because the dot product is zero, the acceleration is always perpendicular to the velocity.

So Coriolis changes the direction of the flow, not its speed.

2. Turn the coupled system into one equation

Differentiate the first equation in time:

\[ \frac{d^2u}{dt^2} = f\,\frac{dv}{dt} \]

Now substitute \((\frac{dv}{dt} = -f\,u)\):

\[ \frac{d^2u}{dt^2} = f(-f u) = -f^2 u \]

So \((u(t))\) satisfies a simple harmonic oscillator:

\[ \frac{d^2u}{dt^2} + f^2 u = 0 \]

By the same steps, \((v(t))\) satisfies: \[ \frac{d^2v}{dt^2} + f^2 v = 0 \]

3. General sol’n (oscillation at frequency \((|f|)\))

A solution to \((\;u'' + f^2 u = 0\;)\) is:

\[ u(t) = A\cos(ft) + B\sin(ft) \]

Use \((\frac{du}{dt} = f v)\) to get \((v(t))\):

\[ \frac{du}{dt} = -Af\sin(ft) + Bf\cos(ft) = f v \]

So

\[ v(t) = -A\sin(ft) + B\cos(ft) \]

4. Apply a common initial condition

Suppose we start with purely eastward flow:

\[ u(0)=U_0,\qquad v(0)=0 \]

At \((t=0)\):

  • \((u(0)=A = U_0)\)
  • \((v(0)=B = 0)\)

So the solution becomes:

\[ u(t) = U_0\cos(ft), \qquad v(t) = -U_0\sin(ft) \]

This is inertial oscillation: the velocity vector rotates with angular frequency \((|f|)\).

The inertial period is: \[ T = \frac{2\pi}{|f|} \]

5. Key property: speed is conserved

Compute the speed:

\[ u^2 + v^2 = U_0^2\cos^2(ft) + U_0^2\sin^2(ft) = U_0^2 \]

So

\[ \sqrt{u^2 + v^2} = U_0 = \text{constant} \]

Interpretation: Coriolis changes the direction of motion but not the magnitude (no energy input or loss).

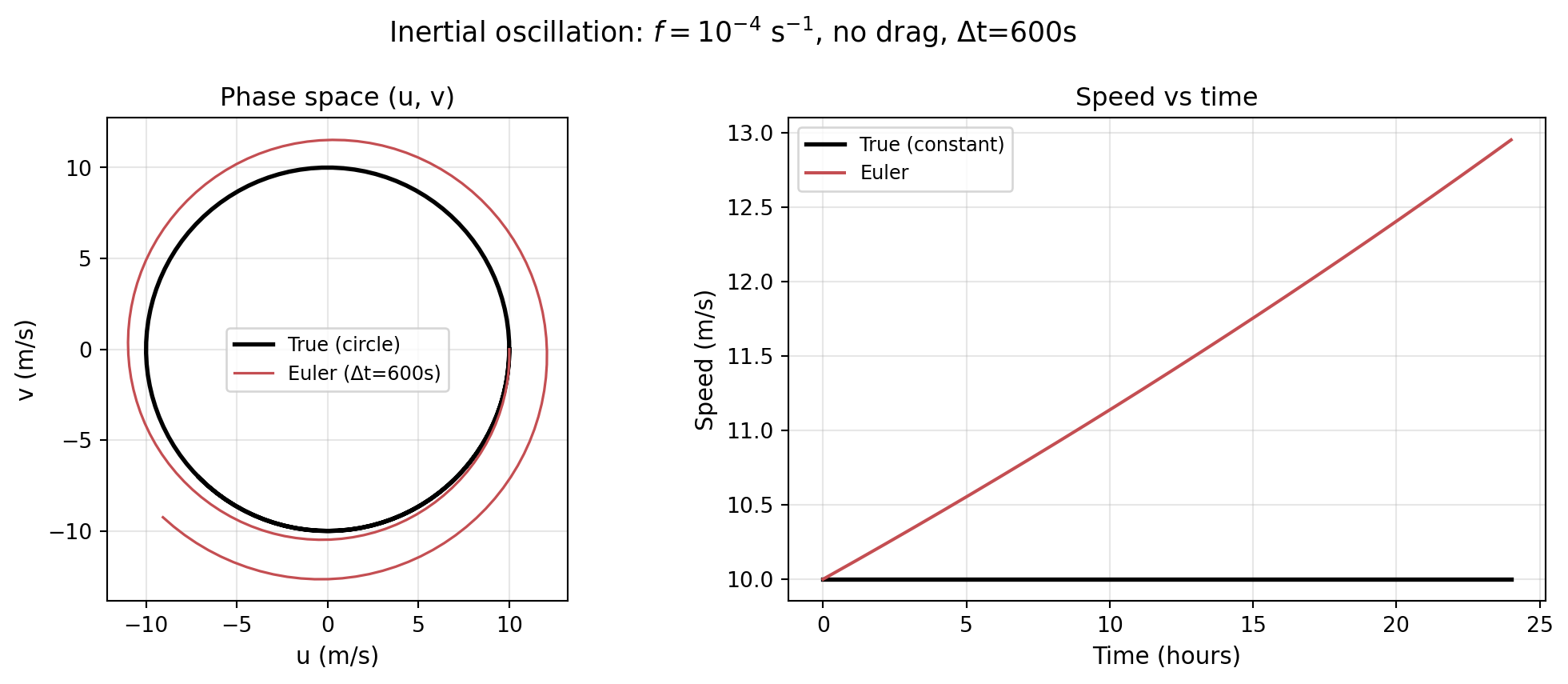
Why Euler Fails: Tangent Steps

Each Euler step follows the tangent to the circle — and lands outside it.

Proof: After one step with \(h = \Delta t\):

\[u_{n+1} = u_n + h f v_n, \qquad v_{n+1} = v_n - h f u_n\]

Compute the new radius squared:

\[R_{n+1}^2 = u_{n+1}^2 + v_{n+1}^2 = (1 + h^2 f^2)\, R_n^2\]

Since \(h^2 f^2 > 0\), the radius always grows:

\[\boxed{R_{n+1} = \sqrt{1 + h^2 f^2}\; R_n > R_n}\]

Forward Euler is unconditionally unstable for pure oscillations.

Euler Spirals Out

:::

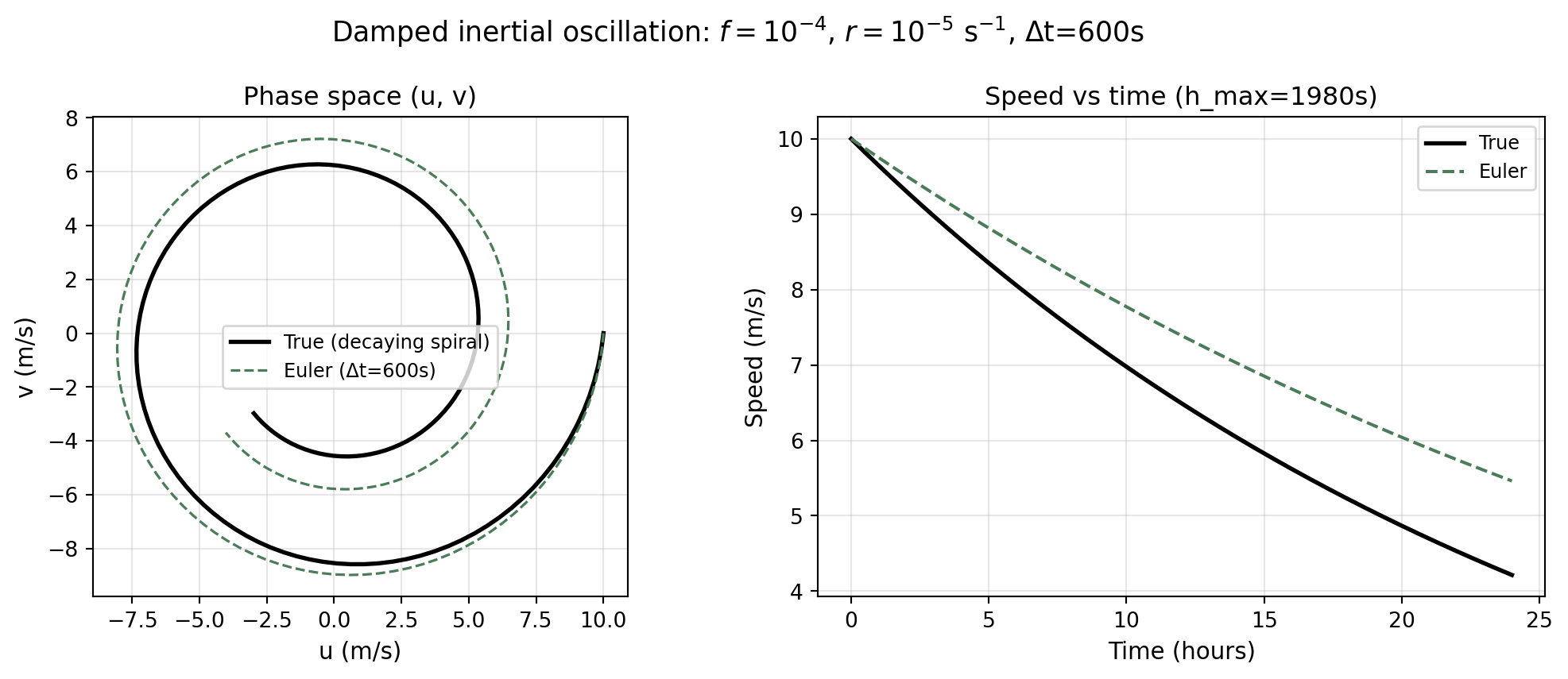
The Fix: Add Drag (Euler Form)

We add linear drag (Rayleigh friction) and integrate with Forward Euler.

Continuous equations: \[ \frac{du}{dt} = f\,v - r\,u, \qquad \frac{dv}{dt} = -f\,u - r\,v \]

1. Forward Euler update

With time step \(h\), Euler says \(N_{n+1} = N_n + h \bullet (tendency)\):

\[ u_{n+1} = u_n + h\,(f v_n - r u_n), \qquad v_{n+1} = v_n + h\,(-f u_n - r v_n) \]

Rewrite to highlight the two effects:

\[ u_{n+1} = (1-rh)\,u_n + (fh)\,v_n, \qquad v_{n+1} = -(fh)\,u_n + (1-rh)\,v_n \]

2) What happens to the radius (speed)?

Define the squared speed (“radius squared”): \[ R_n = u_n^2 + v_n^2 \]

Start from the Euler updates (drag + Coriolis): \[ u_{n+1} = (1-rh)\,u_n + (fh)\,v_n, \qquad v_{n+1} = -(fh)\,u_n + (1-rh)\,v_n \]

Compute the next-step radius: \[ R_{n+1} = u_{n+1}^2 + v_{n+1}^2 \]

Substitute: \[ R_{n+1} = \big[(1-rh)u_n + (fh)v_n\big]^2 + \big[-(fh)u_n + (1-rh)v_n\big]^2 \]

Expand each square: \[ \big[(1-rh)u_n + (fh)v_n\big]^2 = (1-rh)^2u_n^2 +2(1-rh)(fh)u_nv_n +(fh)^2v_n^2 \]

\[ \big[-(fh)u_n + (1-rh)v_n\big]^2 = (fh)^2u_n^2 -2(1-rh)(fh)u_nv_n +(1-rh)^2v_n^2 \]

Add them (cross terms cancel): \[ R_{n+1} = \Big[(1-rh)^2u_n^2+(fh)^2v_n^2\Big] + \Big[(fh)^2u_n^2+(1-rh)^2v_n^2\Big] \]

Factor: \[ R_{n+1} = \Big[(1-rh)^2+(fh)^2\Big]\,(u_n^2+v_n^2) \]

So: \[ \boxed{ R_{n+1} = \Big[(1-rh)^2+(fh)^2\Big]\,R_n } \]

3. Drag can prevent radius growth

For “no expansion” we want \(R_{n+1}\le R_n\), i.e. \(M\le 1\):

\[ (1-rh)^2 + (fh)^2 \le 1 \]

This simplifies to the step-size condition:

\[ -2rh + (r^2+f^2)h^2 \le 0 \quad\Rightarrow\quad \boxed{ h \le \frac{2r}{r^2+f^2} } \]

Interpretation: Euler tends to pump energy into inertial motion; drag removes energy. With small enough \(h\) (or large enough \(r\)), the discrete radius stops growing.

Damped Oscillation!

The Big Picture

System Eigenvalue \(\lambda\) Euler Stability Condition
Pure decay: \(y'=-ay\) \(\lambda = -a\) (real, negative) Conditionally stable \(\Delta t < 2/a\)
Pure oscillation: \(y'=\pm ify\) \(\lambda = \pm if\) (imaginary) Never stable No \(\Delta t\) works
Damped oscillation \(\lambda = -r \pm if\) Conditionally stable \(\Delta t \le 2r/(r^2+f^2)\)

Takeaway for real models:

  • Pure oscillatory modes (gravity waves, inertial oscillations) are poison for Forward Euler
  • Dissipation (friction, diffusion) can stabilize — but only if \(\Delta t\) is small enough
  • This is why weather/climate models use implicit or semi-implicit methods for fast oscillations

Method vs Solver

Method: The mathematical formula/equation

  • Example: Explicit Euler, Runge-Kutta, Adams-Bashforth
  • Defines how to approximate \(y(t)\)

Solver: The software implementation

  • Examples: scipy.integrate.solve_ivp, Julia solve(), our Lorenz63 class
  • Includes: method choice, error control, interpolation, output settings

For this course: We’re building our own solver using Explicit Euler!

Practical Tips

Debugging Your Implementation

  1. Start simple: Test with exponential decay first
  2. Check dimensions: Make sure arrays have correct shapes
  3. Verify tendency: Print out \(f(y)\) for known initial conditions
  4. Compare step sizes: Try \(\Delta t = 0.01, 0.001\) and compare
  5. Visualize: Plot your results - does it look reasonable?

Common Mistakes

Mistake 1: Forgetting to multiply by \(\Delta t\)

# WRONG
y_next = y + tendency

# RIGHT
y_next = y + tendency * dt

Mistake 2: Using wrong state in tendency

# WRONG - using next state before calculating it
tendency = f(y_next)

# RIGHT - use current state
tendency = f(y)

Common Mistakes (cont.)

Mistake 3: Not storing trajectory properly

# WRONG - overwriting instead of appending
for i in range(n_steps):
    state = euler_step(state, f, dt)

# RIGHT - save each state
trajectory = []
for i in range(n_steps):
    state = euler_step(state, f, dt)
    trajectory.append(state)

Summary

Key Takeaways

  1. Most diffEQs don’t have analytical solutions

    • Numerical integration is essential

  2. Explicit Euler is the simplest method: \[y_{n+1} = y_n + f(t_n, y_n) \cdot \Delta t\]

  3. Class structure for ODE solvers:

    • tendency() → rate of change
    • step() → one time step forward
    • integrate() → full trajectory

  4. Apply same pattern to any ODE system

    • Logistic Growth (midterm)
    • Lorenz63 (midterm bonus)

Midterm Checklist

What you need to master:

  • ✓ Derive Euler time stepping from ODE equation
  • ✓ Write pseudo code for LogisticGrowth class
  • ✓ Understand all four class methods (__init__, tendency, step, integrate)
  • ✓ Know Lorenz63 structure (bonus: calculate by hand)
  • ✓ Review NumPy operations (Part 1 of exam)
  • ✓ Review Python fundamentals (Part 2 of exam)

Study Resources

Practice materials:

  • Simple exponential decay implementation
  • Review Lorenz63 class from lecture notes

Get help:

  • Office hours: Will (Tu/Th 11:15-12:15p), Aiden (M/W 3:30-4:30p)
  • Practice writing pseudo code
  • Test your understanding by explaining to a classmate

Questions?

Final tips:

  • Focus on understanding, not memorization
  • Practice the class structure pattern
  • Start with simple examples, build up complexity
  • Draw diagrams to visualize time stepping

You’ve got this! The concepts are straightforward once you see the pattern.

Acknowledgments

Course materials adapted from:

Fiona Majeau, ECEN 5447: Power System Dynamics, CU Boulder

Thank you for the excellent numerical integration materials!